Rubiks Cube
English | Deutsch
- Anleitung für den 3x3x3-Würfel
- Anzahl der möglichen Konstellationen
- Anleitungen für weitere Rätsel (Links)
Anleitung für den Zauberwürfel (3x3x3)
Anmerkung
Diese Anleitung bezieht sich auf den „Original“-Zauberwürfel, bei dem oben Weiß liegt, die Seiten Rot, Grün, Blau und Orange sind und dessen Unterseite Gelb ist. Wessen Würfel nicht so aussieht, muss sich die Farbbenennungen passend umdenken.
0. Vorarbeit
Jeder, der sich ein wenig mit dem Zauberwürfel beschäftigt hat, sollte in der Lage sein, eine einzelne Farbseite korrekt zusammenzustellen. Mit ein bisschen mehr Arbeit ist es auch leicht möglich, den ersten Ring der zu der gerade erstellten Seite benachbarten Seiten richtig zusammenzustellen.
Im Folgenden wird davon ausgegangen, dass die Spielerin mit der weißen Seite angefangen hat; prinzipiell funktioniert es natürlich auch mit jeder anderen Seite, aber dann passen einige der hier benutzten Farben nicht mehr.
Man hat nun also die weiße Fläche sowie den ersten Ring der benachbarten vier Flächen fertig.
Die weiße Fläche zeigt nach oben. Durch Drehen des mittleren Ringes kann man die Mittelsteine passend zum ersten Ring anordnen, dies funktioniert immer.
1. Der zweite Ring
Jetzt sollen die Kantenstücke des zweiten Rings richtig
angeordnet werden. Die hier fehlenden Stücke befinden sich
entweder auf dem untersten Ring oder sie sitzen irgendwo im
mittleren Ring.
Ein einzelnes einzufügendes Stück wird
wie folgt positioniert:
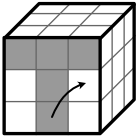








oder:
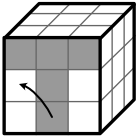








Sitzt ein Kantenstück bereits an der richtigen Stelle, allerdings falsch herum, so muss zunächst ein anderes Stück dort eingefügt werden.
Nachdem alle Kantenstücke so bearbeitet worden sind, sind die ersten beiden Ringe fertig.
2. Plazieren der gelben Kantenstücke
Der Würfel wird nun so gedreht, dass die gelbe Fläche oben liegt. Als nächsten sollen die Kantenstücke der gelben Fläche an die richtige Stelle gebracht werden; dazu werden jeweils zwei Kantenstücke paarweise vertauscht:
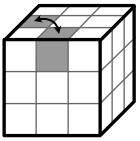







3. Kippen der Kantenstücke
Nun müssen die Kantenstücke noch gekippt werden, damit die gelbe Seite nach oben zeigt. Dazu wird der Würfel so gehalten, dass der zu kippende Stein rechts liegt:
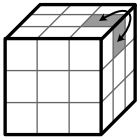








Nach diesen Zügen kann der Würfel etwas chaotisch aussehen, aber das macht zunächst nichts.
Ist ein Stück auf diese Weise gekippt worden, so wird nur die oberste Ebene so weiter gedreht, dass der jetzt zu bearbeitende Stein wieder rechts liegt.
Wenn alle Kantensteine so bearbeitet worden sind, sollte der Würfel wieder normal aussehen.
Hierzu der Hinweis von Franco Erpf:
Unter einer bestimmten Konstellation funktioniert das nicht:
Situation: Die gelbe Seite ist oben, die Kantenstücke sind schon alle an der richtigen Stelle, aber während zwei Kantenstücke schon richtig gekippt sind, sind die anderen beiden, gegenüberliegenden Kantenstücke beide falsch gekippt. Wenn man nun den hier beschriebenen Schritt 3 ausführt, dann sind danach alle vier Kantenstücke gekippt, d.h. die ursprünglich falsch gekippten beiden sind nun richtig, dafür sind die vorher schon richtigen beiden Kantenstücke nun falsch gekippt. Dieser Vorgang lässt sich nun beliebig oft wiederholen.
Die Lösung:
Mit Hilfe der Zugfolge aus Schritt 1 eines der Kantenstücke herausdrehen. Den Würfel um 90 Grad drehen (Gelb liegt auf der Seite) und das herausgedrehte Stück von der anderen Seite her mit der entsprechenden Schirtt-1-Zugfolge wieder einfügen. Danach lässt sich wieder mit Schritt 3 fortfahren.
4. Plazieren der Ecken
Danach sollen die Ecksteine an die richtige Stelle gebracht werden. Diese Zugfolge wurde mit von Volker Bartels zugesandt.
Die Eckstücke werden einzeln in die richtige Position gebracht:
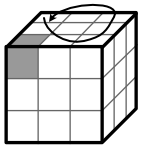 A: Richtige Ecke liegt links vorne und die
Ecke rechts vorne muss nach rechts hinten:
A: Richtige Ecke liegt links vorne und die
Ecke rechts vorne muss nach rechts hinten:








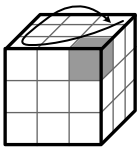 B: Richtige Ecke liegt rechts vorne und die
Ecke links vorne muss nach links hinten:
B: Richtige Ecke liegt rechts vorne und die
Ecke links vorne muss nach links hinten:








Sollte keine Ecke richtig liegen, einfach eine der ersten beiden Möglichkeiten drehen, danach sollte eine Ecke richtig liegen.
5. Kippen der Ecken
Als letztes müssen die Ecksteine noch richtig gekippt werden. Dazu wird der Würfel so gehalten, dass ein zu kippendes Stück vorne rechts liegt.
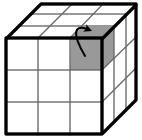
Variante 1: Gelb muss von vorne nach oben:








Variante 2: Gelb muss von der rechten Seite nach oben:
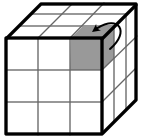








Auch hierbei gilt, dass der Würfel zwischendurch recht konfus aussehen kann und dass zur Bearbeitung der nächsten Ecke nur die oberste Ebene gedreht wird.
Wenn man weniger Züge auswendig lernen will, dann kann man auch nur eine der beiden Varianten lernen und diese dann ggf. einmal wiederholen, falls gelb ungünstig lag.
Wurden alle Züge richtig ausgeführt, so ist der Würfel nun fertig!
Anzahl der möglichen Kombinationen
Ein paar Leute haben mich gefragt, wie viele Kombinationen der Würfel hat, d. h. auf wie viele verschiedene Arten die einzelnen Steine stehen können. Hier ist meine Antwort:
Die Mittelsteine der Flächen sind untereinander fest verbunden. Sie können ihre Position untereinander nicht verändern. Im folgenden nehme ich an, dass diese Mittelsteine immer an der selben Stelle bleiben, also z. B. weiß oben und blau vorne, wodurch sich die Position der anderen Mittelsteine eindeutig ergibt. Im mathematischen Sinne wären alle weiteren Kombinationen, die sich nur dadurch unterscheiden, wie man den Würfel hält, identisch und somit uninteressant.
Alle anderen Steine sind hingegen wesentlich interessanter. Es gibt nämlich keine zwei gleichen Steine. Und jeder Stein kann an jeder beliebigen Stelle (für die er prinzipiell geeignet ist) auftauchen und kann dabei jede Orientierung einnehmen, die seine farbigen Seiten erlauben.
Im Einzelnen:
Die Ecksteine.
Wollte man den Würfel aus Einzelteilen zusammenbauen, so hätte man für den ersten Eckstein 8 mögliche Positionen (denn soviele Ecken gibt es nun einmal). Außerdem könnte man sich für eine von drei Orientierungen entscheiden (wenn es sich um eine obere Ecke handelt: Welche der drei Farben soll nach oben? Wenn es sich um eine untere Ecke handelt: Welche der drei Farben soll nach unten?)
Somit ergeben sich 8 * 3 = 24 Möglichkeiten, den ersten Stein zu setzen. Danach gibt es für den nächsten Eckstein nur noch 7 freie Plätze, aber immer noch drei mögliche Orientierungen. Der Stein danach hat nur noch 6 Plätze zur Auswahl und so weiter.
Es ergibt sich: Möglichkeiten, die Ecken einzubauen: (8 * 3) * (7 * 3) * (6 * 3) * ... * (1 * 3) = 8! * 38 = 40320 * 6561 = 264.539.520.
Die Kantensteine
Die Kantensteine berechnen sich ähnlich. Es gibt 12 Steine, und jeder hat zwei mögliche Orientierungen. Somit: (12 * 2) * (11 * 2) * ... * (1 * 2) = 12! * 212 = 479001600 * 4096 = 1.961.990.553.600.
Das Endprodukt
An sich würde es jetzt genügen, diese beiden Werte zu multiplizieren (was ich zunächst auch annahm). Aber Robert Staatz machte hierzu folgende Anmerkungen:
„Die oben angegebene Anzahl kann nur erreicht werden, wenn der Würfel auseinander genommen wird und dann 'blind' zusammengesetzt wird.
Die richtige Anzahl der Kombinationen ist um Faktor 12 geringer, also:
(12! * 212) * (8! * 38) / 12
Begründung:
- (Divisor 2) Es ist nicht möglich zwei Ecken zu tauschen, wenn die Kanten an der gleichen Stelle bleiben sollen. Es gibt zwar andere Algorithmen zum Sortieren in denen zwei Ecken getauscht werden können, dann lassen sich aber nicht zwei Kanten miteinander vertauschen.
- (Divisor 2) Es ist nicht möglich eine Kante zu kippen ohne das andere Kanten in Mitleidenschaft gezogen werden.
- (Divisor 3) Es ist auch nicht möglich das eine einzelne Ecke verdreht ist.“
Es ergibt sich: 264.539.520 * 1.961.990.553.600 / 12 = 43.252.003.274.489.856.000 Möglichkeiten
Ausgeschrieben wären dass: Dreiundvierzig Trillionen, zweihundertzweiundfünfzig Billiarden, drei Billionen, zweihundertvierundsiebzig Milliarden, hierhundertneunundachtzig Millionen achthundertsechsundfünfzig Tausend.
David Buder hat darauf hingewiesen, dass in der Gebrauchsanleitung seines Würfels die Anzahl der Konstellationen mit 519.024.039.293.878.272.000 angegeben wird - also ohne den Divisor 12. Diese Angabe dürfte aber falsch sein. In seinem Buch „Cubed - Der Zauberwürfel und die großen Rätsel dieser Welt“ schreibt Ernö Rubik selbst, die Anzahl der möglichen Stellungen sei 43 Trillionen, ohne dies weiter herzuleiten.
Lösung mit wenigsten Zügen
Durch einen Artikel von Wolfgang Blum in der Süddeutschen Zeitung wurde ich auf einige aktuelle Forschungen zum Zauberwürfel aufmerksam. Es stellt sich die Frage:
Wie viele Züge benötigt man mindestens und höchstens,
um den
Würfel in einer beliebigen Stellung zu lösen?
Die gesuchte Zahl wird von den Fans auch als „Gottes Zahl“ bezeichnet, wobei ich das angesichts anderer Zahlen wie π, e oder der Lichtgeschwindigkeit c doch etwas vermessen (oder gar blasphemisch) finde.
Aber zurück zum Thema. Gezählt werden übrigens hierbei als Zug Drehungen sowohl um 90° als auch um 180° - wenn man nur 90°-Drehungen zuließe, wäre die Minimalzahl höher.Michael Reid aus Florida hat bereits 1993 eine Konstellation demonstriert, aus der beweisbar ist, dass mindestens 20 Züge zur Lösung notwendig sind. Es existiert also schon mal eine Untergrenze für die minimale Anzahl von Schritten. Aber gibt es kompliziertere Konstellationen, für die mehr Züge notwendig sind?
Im März 2008 war der aktuelle Stand die Arbeit von Tomas Rokicki, der die Obergrenze schrittweise auf 22 begrenzen konnte. Somit muss die gesuchte Zahl also irgendwo zwischen 20 und 22 liegen. Rokicki ließ nicht locker und schaffte es 2013 schließlich, durch ein paar Zerlegungen des Problems und Rückgriff auf massive Rechenkraft zu beweisen, dass sich der Würfel tatsächlich aus jeder Position in genau 20 Zügen lösen lässt. Mehr dazu auf cube20.org.
Weitere Lösungen
Ansonsten habe ich hier nur die Lösung für den 3x3x3 Würfel, aber es gibt noch mehr Puzzles. Weitere Lösungen findet ihr über die Rubik's-Homepage. Viel Spaß!
Weitere Links:
- Rubik's Cube Info: Verschiedene Lösungsstrategien